一些套路的总结

  1. 分解问题的角度：固定某一个维度，尝试另一维度上的所有可能
    • 可能是array的(i, j) pointers
    • 可能是矩形的长与宽
    • 可能是tree的每一个subtree，比如固定左子树，来遍历每一个可能的右子树
    • 可能是情景题的每一对pair
  2. 求所有解的，一 般暴力上backtracking
  3. 如果问最短/最少的, 先想BFS和DP
  4. 如果环相关，或者涉及到重复访问，可以使用DFS + visited state（或者记忆数组）
  5. 如果问连通性, 静态靠DFS/BFS, 动态靠Union-Find
  6. 如果不同的实例或者节点之间有依赖性, 想想Topologic order 和indegree
  7. DAG的万能套路：先进行DFS+memo, 再考虑如何转化成DP
  8. 建图的时候想想vertex, edges/neighbors, cost分别是什么。如果出现cycle, 别忘了给vertex增加状态（visited）
  9. 树相关, 记得考虑backtracking 和 pure recursion两条路
  10. 遇到字符串/字典/char board相关的, Trie tree（前缀树）总是可以试试的
  11. Range里求最大/最小/sum等特征值, Segment tree（线段树）会是不错的选择
  12. Matrix和Array通常都是
    • Two Pointers
    • Sliding Window(fixed & not fixed)
    • DP
  13. DP题型往往是
    • 问你可不可以啊, 数量有多少啊 -> 使用bool类型的数组
    • 两个string上match来match去的 -> 二维数组，两个维度分别为两个string的长度
    • 1D/2D array 相关
    • 博弈游戏 -> 考虑可以往前多少步可以找到相关状态
  14. 破解DAG cycle想想哪个维度是具有单调性的: 常见的steps, directions, paths
  15. Reversed idea非常重要, 可能会帮助你破题: 最长可能是某种最短的反面, 最多可能是某种最少的反面, obstacle的反面是reachable, subarray的反面是array中的剩下元素, left的反面是right
  16. Look up别忘了HashMap/HashSet（HashMap + DLL是常见hybrid数据结构）
  17. 找规律试试那些旁门左道: 单调Stack/双端Deque
  18. 数组相关，而且涉及到元素之间大小比较的，可以先考虑是否可以先进行排序
  19. 时空复杂度
    • backtracking相关, 想想branching factor和height
    • DFS+memo/DP相关, 想想state数量, 以及每个state的cost
    • tree相关, 总是要考虑balanced 和 single linked list的
    • array/矩阵相关, 先数数你有多少个for loops
    • binary search application相关, 别忘了check function开销
    • stack/queue/deque相关, 常说的吃进去一次又吐出来一次
    • Java的string是朵奇葩, string concatenation不是免费的 -> O(n)
    • 没人知道n是什么, 先告诉别人m，n，k，V，E是什么
  20. 比较不同sol的trade offs
    • Time/Space complexity异同
    • online/offline算法(online算法表示可以一直有数据传输进来的方法)
    • pre-computation cost，预处理
    • 不同APIs的call frequency差异会导致不同的时间要求
    • extension: 是否适用于generic parameters/stream input
    • 线程安全/large scale

DP问题的一些总结

DP有六步，建议面试时写在白板上，一步都不能少，基本上你写出这些 implement起来也非常简单了

  1. definition: dp(i)或者dp(i, j) 表示什么含义，比如largest subarray sum ending at arr(i), and must include arr(i)，注意语言描述，包括还是不包括arr(i)/matrix(i, j)；
  2. induction rule: dp(i) 的 dependency 是怎么样的，依赖于dp(i-1) 还是 dp(i+1) 还是 dp(k) for all k < i or all k > i 等等，试着过几个小例子推导一下；
  3. base case: 往往是dp(0)，二维往往是第一行， 第一列，也就是dp(i, 0)和dp(0, j)；
  4. result: 往往是dp(n), max(dp(i)) 等等, 从definition 出发；
  5. filling order: 也就是你填dp表格的顺序，从induction rule 的 dependency出发，判断是从左到右还是从左上到右下；
  6. optimized: 分为时间和空间两方面：
    • 时间的比较难，因为往往需要你重新define dp state 和 induction rule；
    • 空间比较简单，可以根据induction rule看出来，比如斐波那契数列: dp = dp(i-1) + dp(i-2), 那么dp(i) 只依赖于前两个元素，就不需要create 整个 dp array，两个variable即可，空间可以从O(n)优化到O(1)。

14种常见模式

滑动窗口

滑动窗口主要就是维护一个可以不断变化左右边界的子数组，如下图所示：

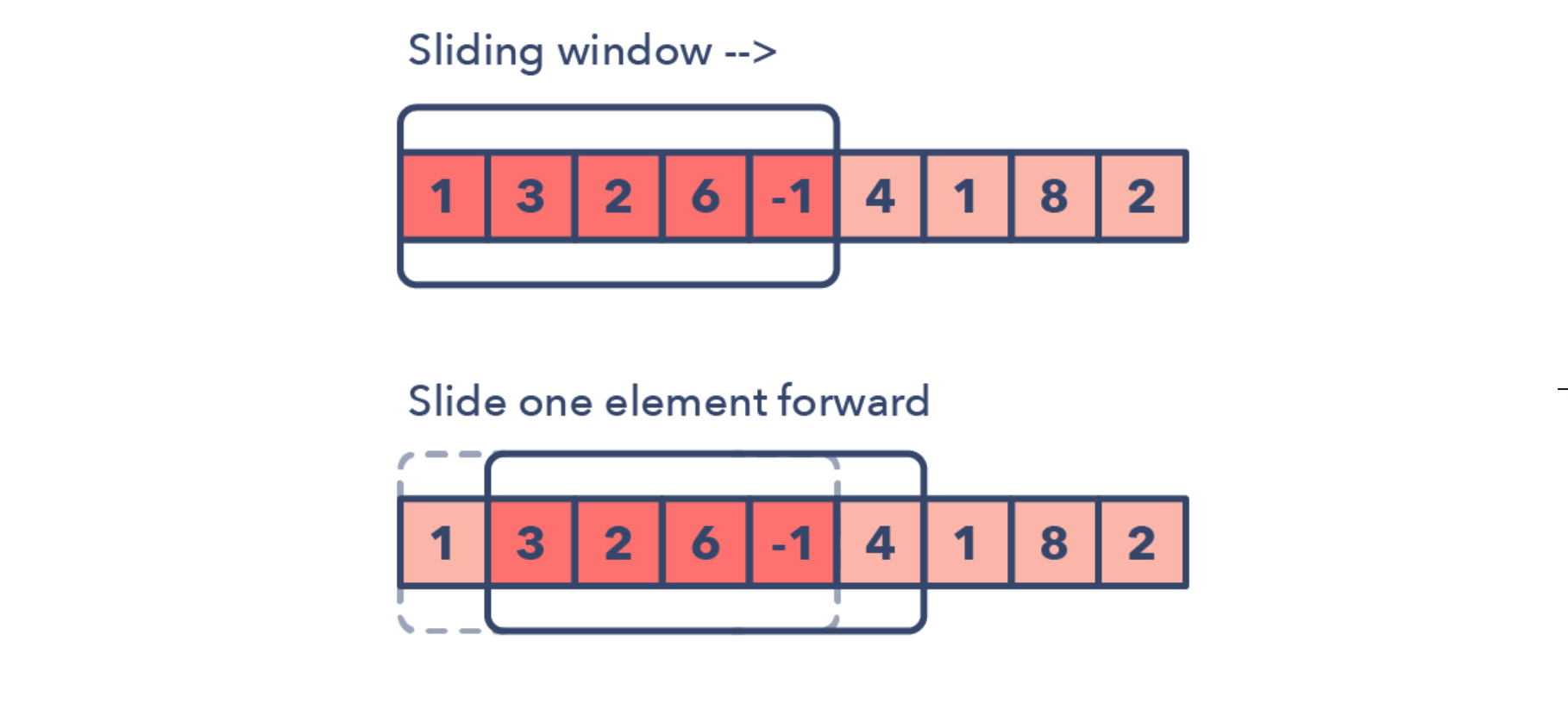
slidingWindow

每一次该窗口左边界右移一格，右边界根据需要进行相应的变化，可能向左移动，可能向右移动，也可能不变。

滑动窗口的问题的标志
  1. 输入是线性的结构，比如链表、数组和字符串
  2. 被要求求解最长或者最短的子字符串，子数组或者特定值
常见问题
  1. Maximum sum subarray of size ‘K’ (easy)
  2. Longest substring with ‘K’ distinct characters (medium)
  3. String anagrams (hard)

双指针

双指针主要是同时使用两个指针迭代遍历数据结构，直到其中一个或者两个指针达到特定状态。一般用于有序的数组或者链表，可以将原本的O(n^2)​的复杂度降低成​O(n)​。

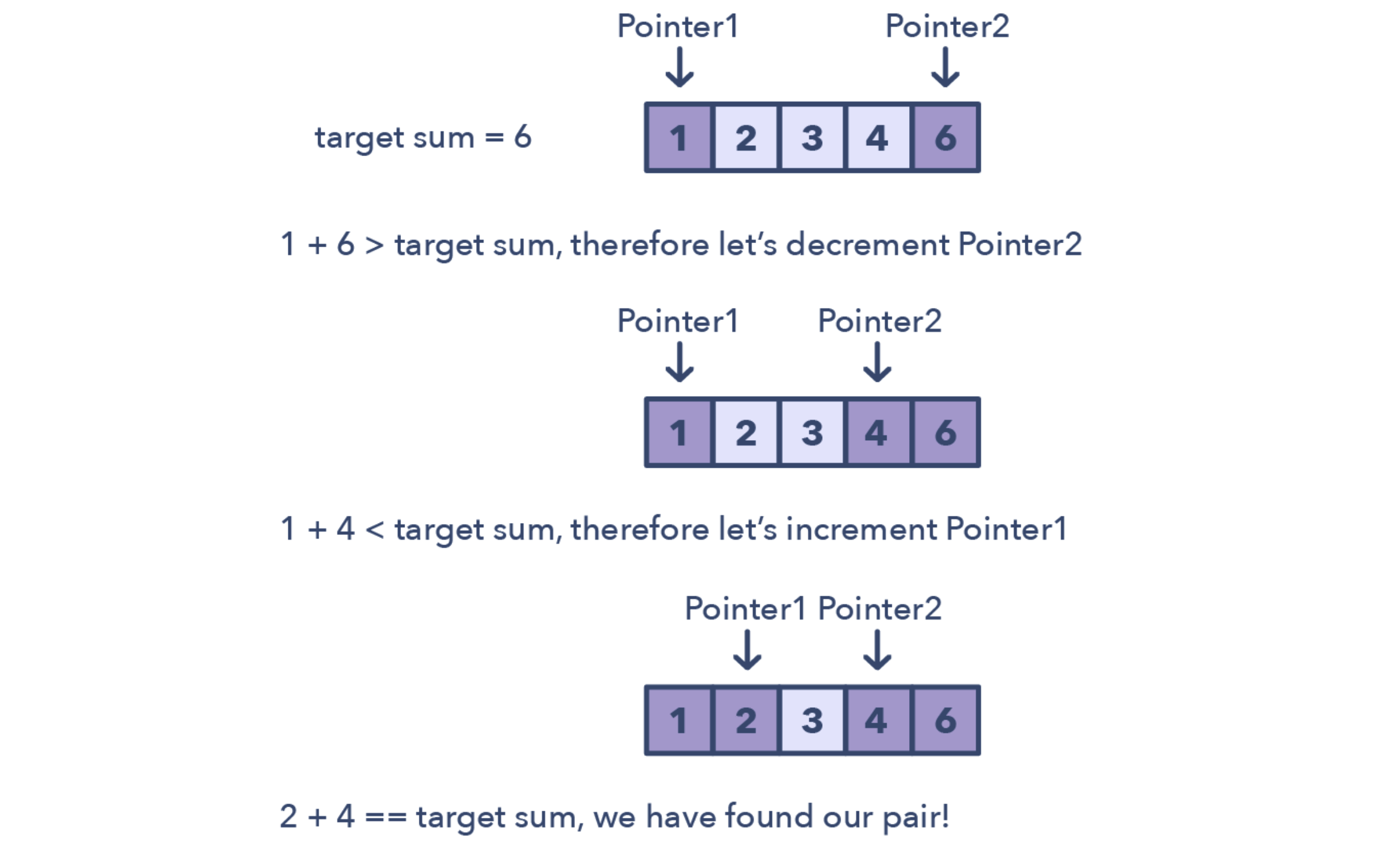
TwoPointer

双指针问题的标志
  1. 在有序数组或者链表中找到一系列满足特定条件的元素
  2. 这一系列元素一般成对(pair)、成三对(triplet)或者子数组(subarray)
常见问题
  1. Squaring a sorted array (easy)
  2. Triplets that sum to zero (medium)
  3. Comparing strings that contain backspaces (medium)

快慢指针

又称Hare & Tortoise algorithm，是一种使用不同行进速度的双指针的算法，经常用在处理环形链表的问题上。如果两个指针都在同一个环上，则快指针一定能和慢指针相遇。

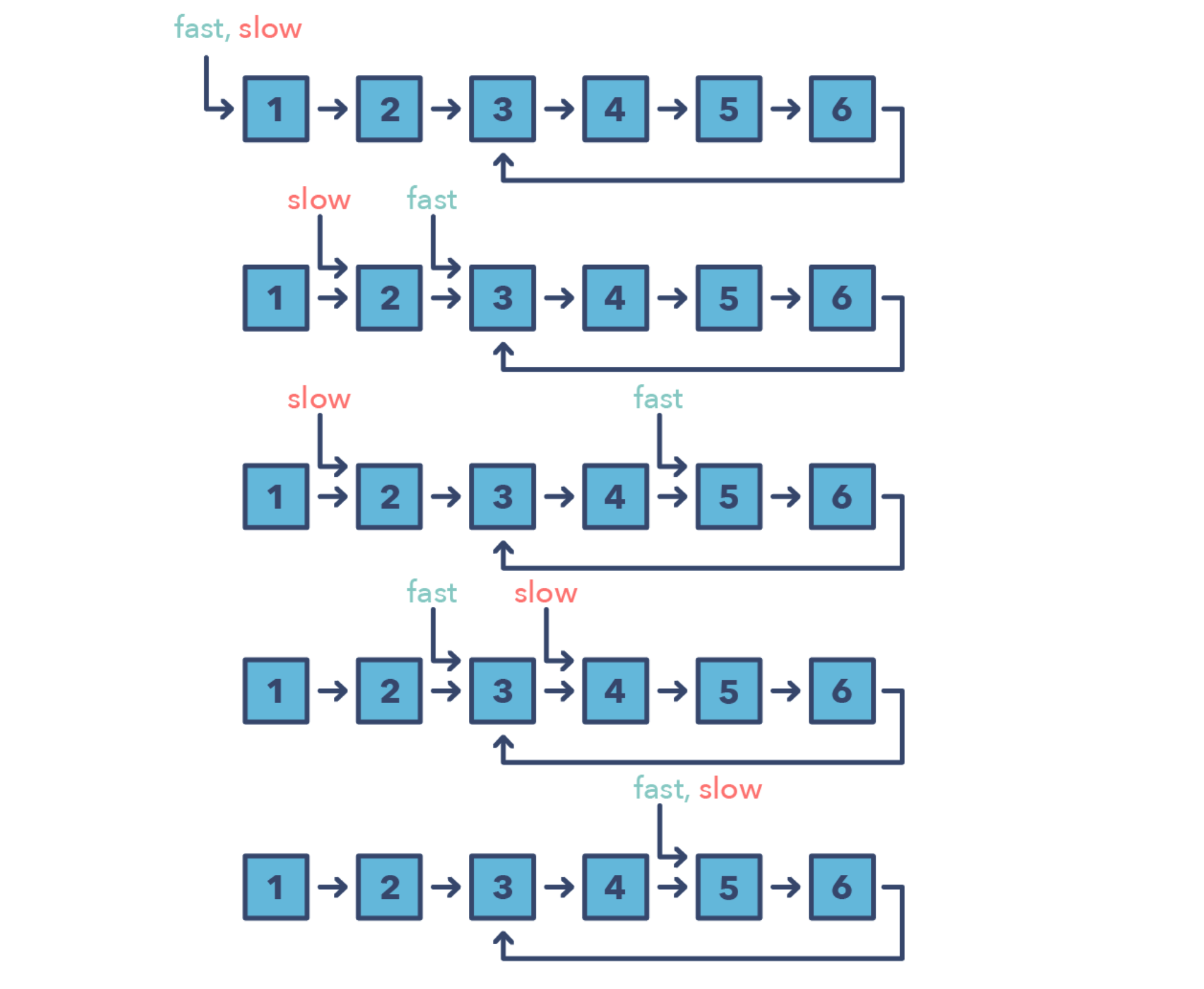
Fast&SlowPointer

快慢指针问题的标志
  1. 一般是带环的链表或者数组
  2. 需要知道特定元素的位置，或者整个链表的长度
  3. 一般不用在单项链表等无法回头的结构中
主要问题
  1. Linked List Cycle (easy)
  2. Palindrome Linked List (medium)
  3. Cycle in a Circular Array (hard)

区间的合并

区间合并主要是用来处理相互重叠的区间问题的，主要有以下六种情况：

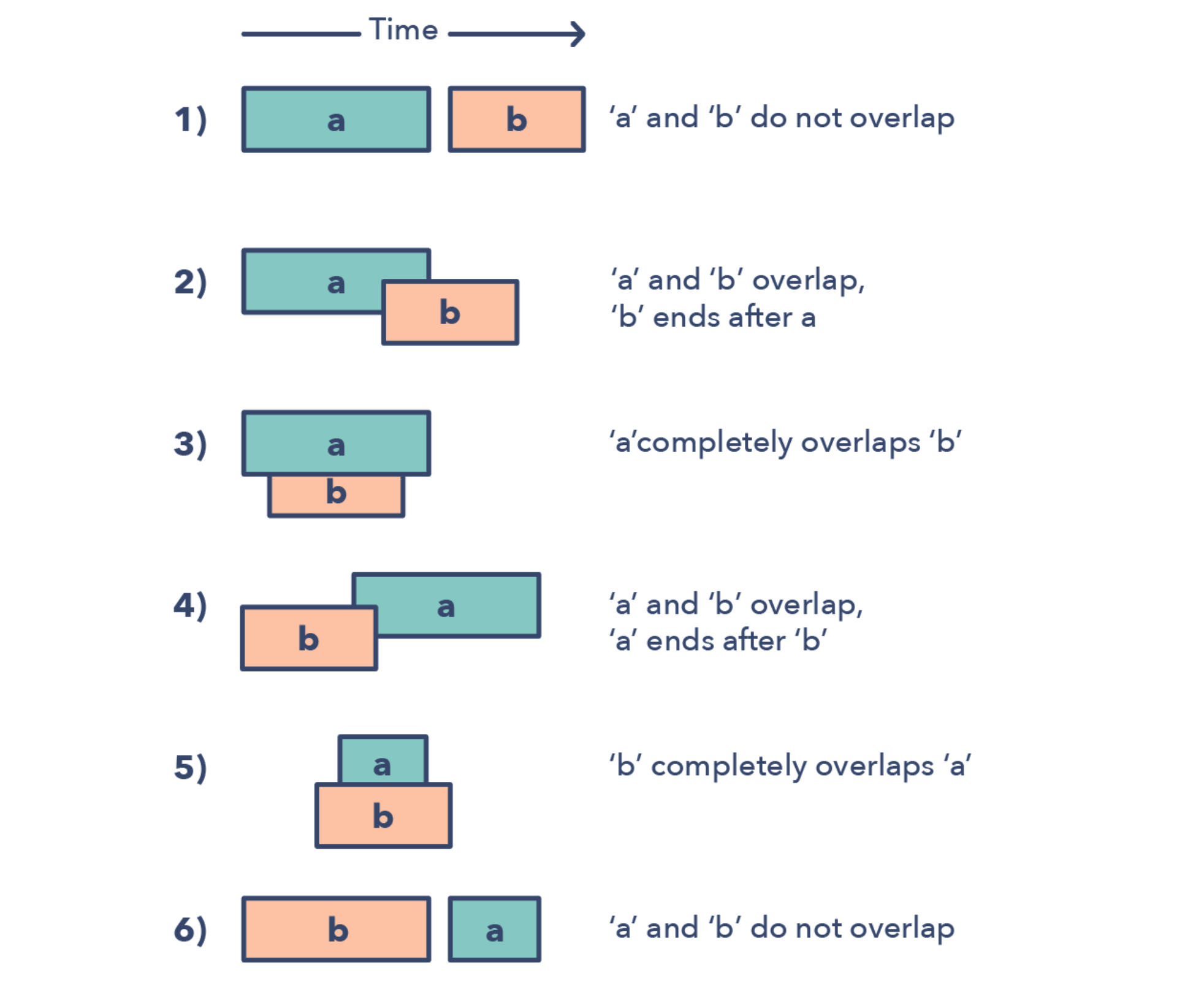
MergeIntervals

区间合并问题的标志
  1. 需要产生只包含互斥区间的数组
  2. 看到“overlapping intervals”的时候
主要问题
  1. Intervals Intersection (medium)
  2. Maximum CPU Load (hard)

循环排序

主要处理数组中的数值限定在一定的区间的问题。

CyclicSort

循环排序问题的标志
  1. 涉及到排序好的数组，而且数值满足于一定的区间
  2. 需要在排好序/翻转过的数组中，寻找丢失的/重复的/最小的元素
主要问题
  1. Find the Missing Number (easy)
  2. Find the Smallest Missing Positive Number (medium)

原地链表翻转

原地链表翻转就是要利用提供的链表的空间来对链表进行翻转操作，一般需要多个变量：

  • current指向当前遍历到的节点
  • previous指向上一个处理好的节点

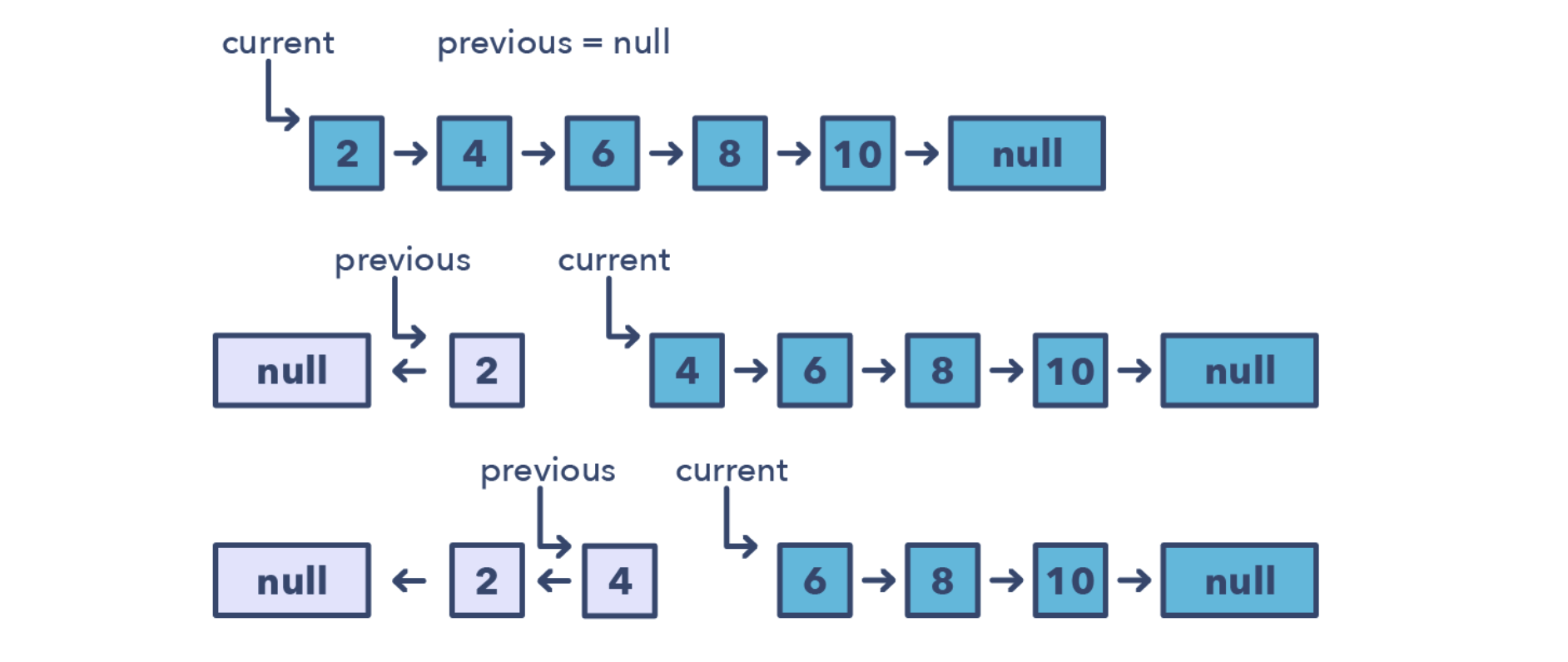
ReverseLinkedList

原地链表翻转的标志
  • 被要求不使用格外空间进行链表的翻转
主要问题
  1. Reverse a Sub-list (medium)
  2. Reverse every K-element Sub-list (medium)

树BFS

在树上使用BFS

树BFS的标志
  • 需要一层一层的遍历树的时候
主要问题
  1. Binary Tree Level Order Traversal (easy)
  2. Zigzag Traversal (medium)

树DFS

在树上使用DFS

树DFS的标志
  1. 需要按前中后序遍历树的时候
  2. 需要搜索的节点离叶节点更近的时候
主要问题
  1. Sum of Path Numbers (medium)
  2. All Paths for a Sum (medium)

双堆

双堆，即一个最大堆一个最小堆，各存放数组的一般的内容

双堆问题的标志
  1. 优先队列或者scheduling相关的问题
  2. 找一组数中的最大/最小/中间的数
  3. 具有二叉树结构的时候
主要问题
  • Find the Median of a Number Stream (medium)

子集问题模式

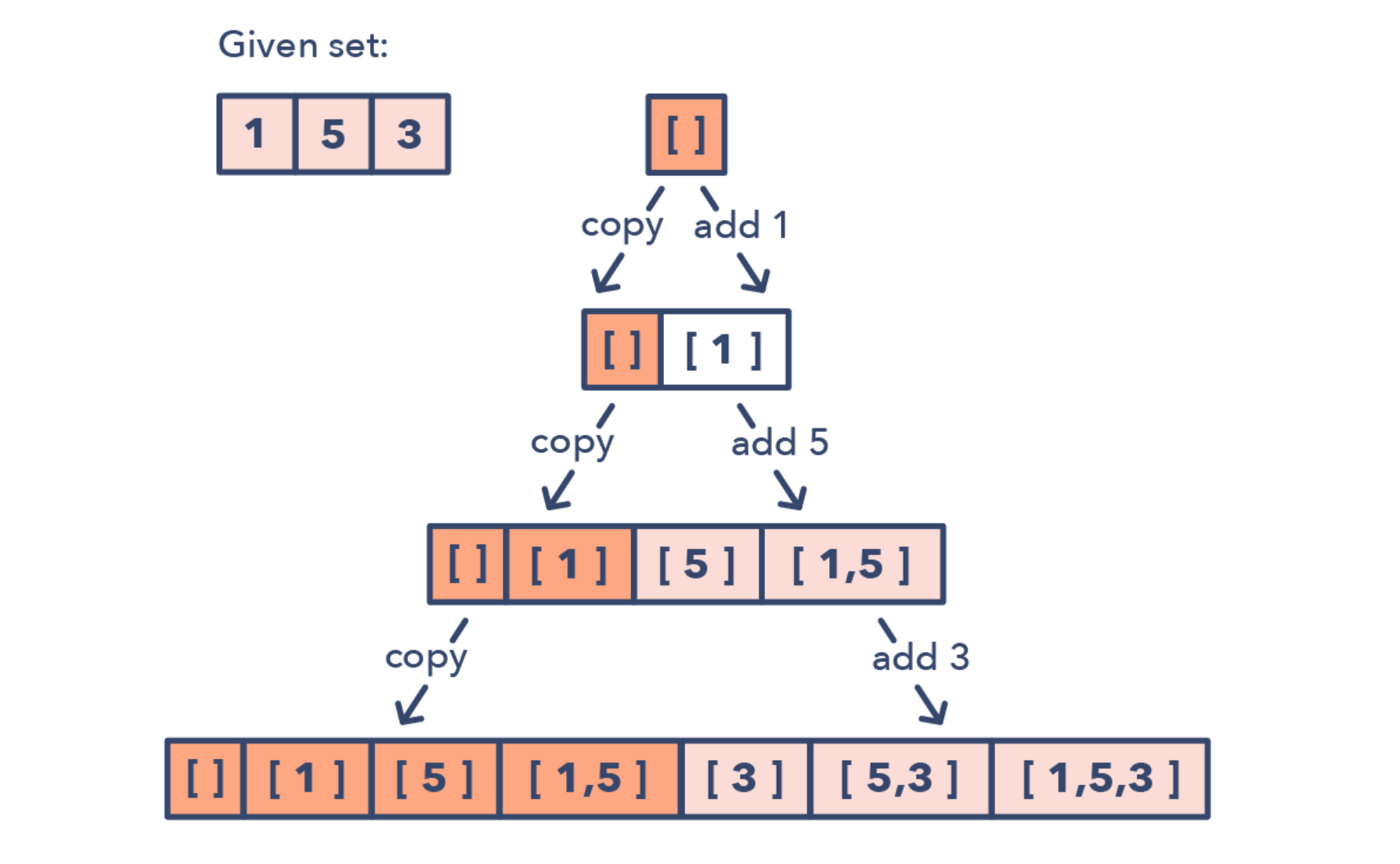
Subset

子集问题模式的标志
  • 需要找数字的排列或者组合
主要问题
  1. Subsets With Duplicates (easy)
  2. String Permutations by changing case (medium)

二分

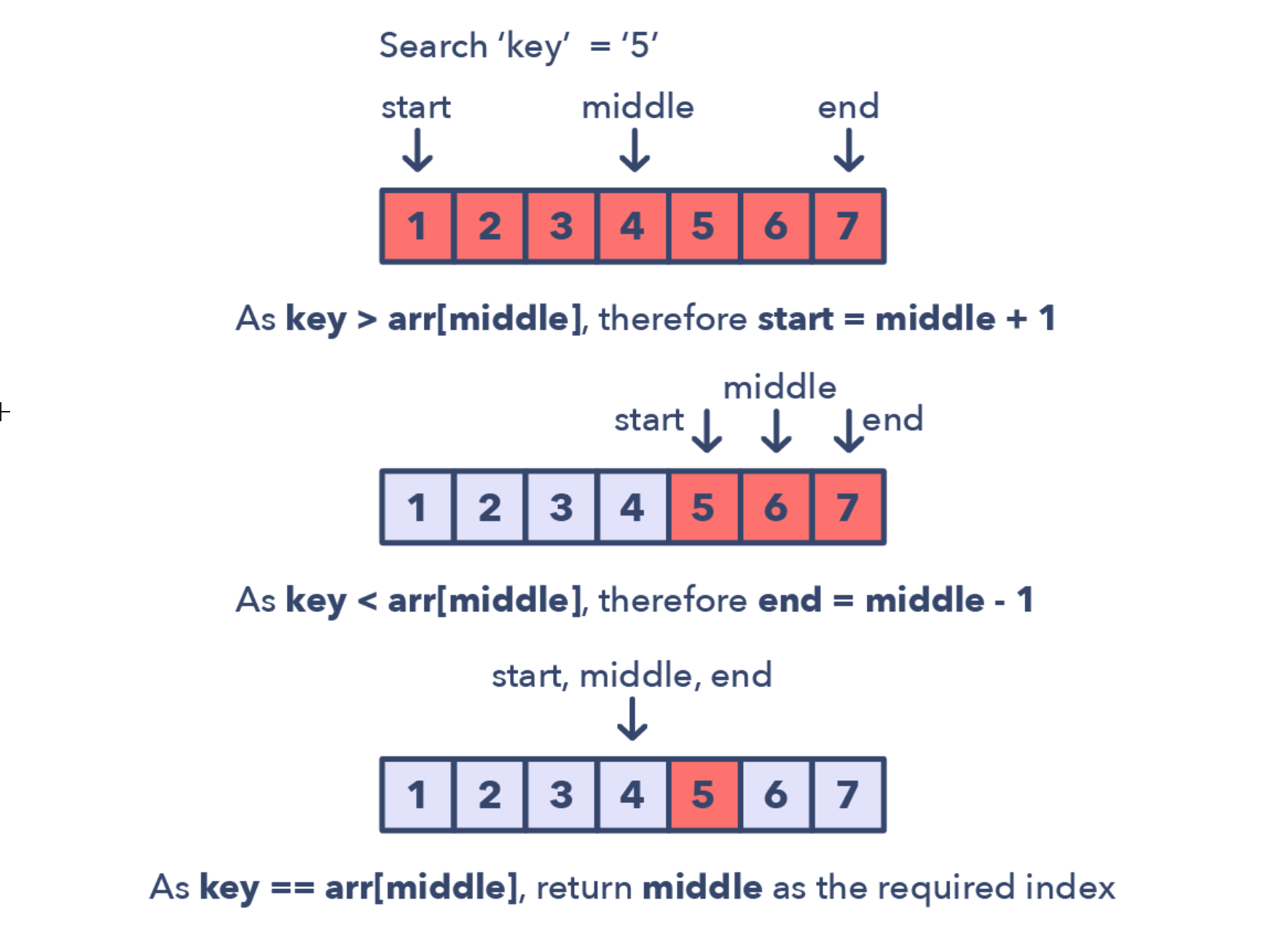
Binary

主要问题
  1. Order-agnostic Binary Search (easy)
  2. Search in a Sorted Infinite Array (medium)

前k大的元素

主要用于求解前k大/小的元素，一般采用最大堆或者最小堆的方式

TopK

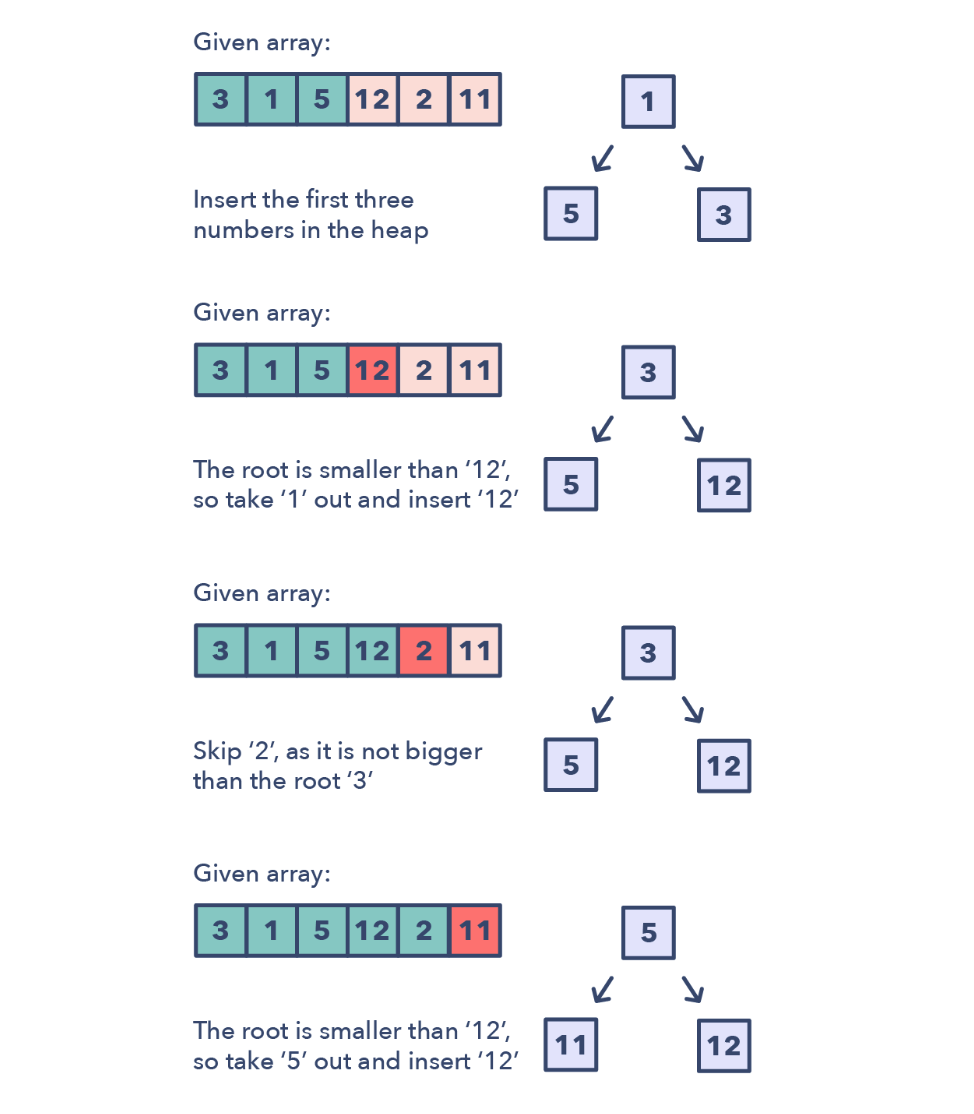
topK的标志
  1. 需要求解最大/最小/最频繁的元素
  2. 通过排序定位特定元素
主要问题
  1. Top ‘K’ Numbers (easy)
  2. Top ‘K’ Frequent Numbers (medium)

K路归并

主要涉及到k个有序数组的合并

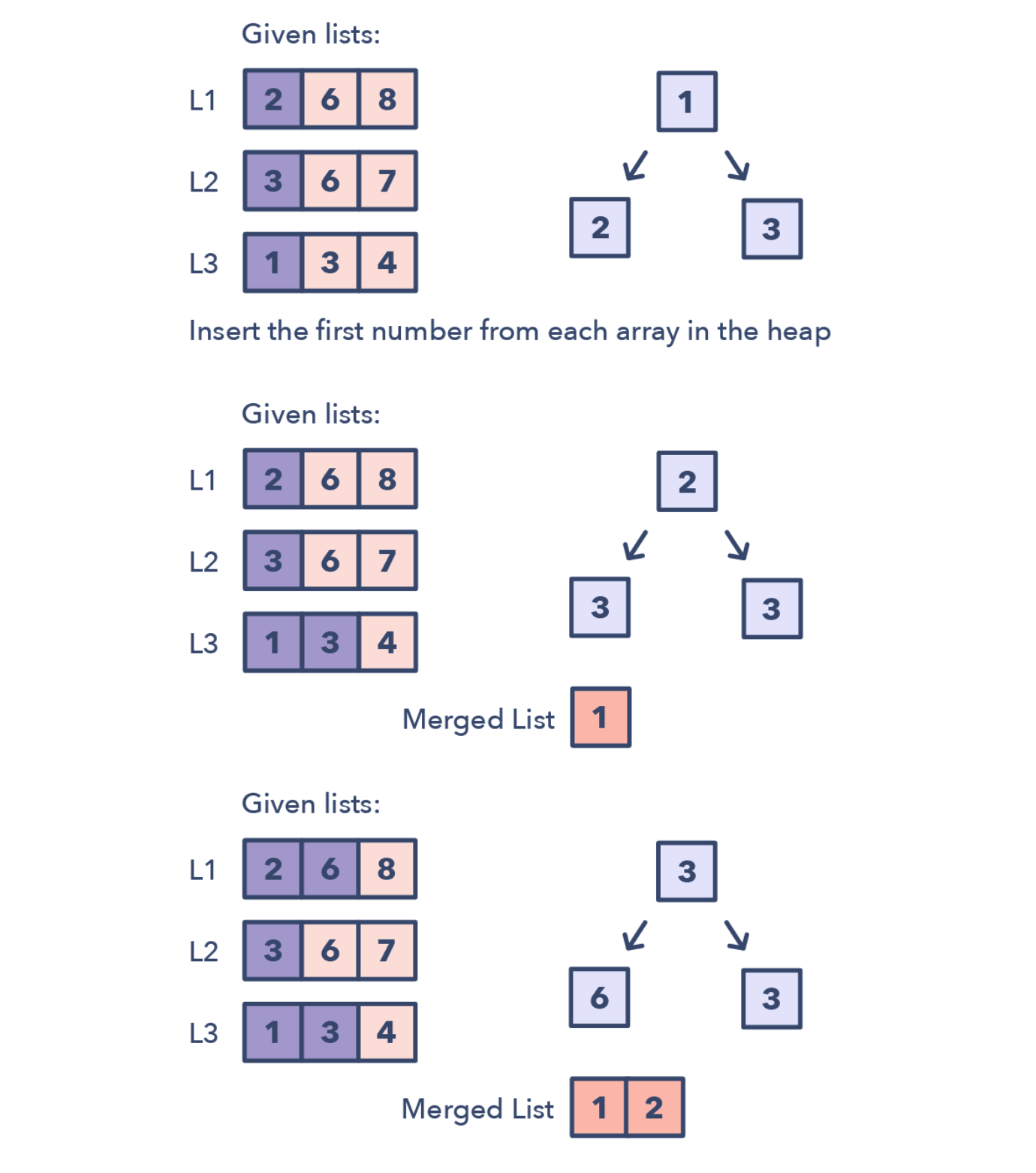
KMerge

K路归并的标志
  1. 输入是排好序的数字，链表或者矩阵
  2. 需要合并多个排好序的数组，或者是找到这些数组中的最小数
主要问题
  1. Merge K Sorted Lists (medium)
  2. K Pairs with Largest Sums (Hard)

拓扑排序

  1. 初始化
    a) 借助于HashMap将图保存成邻接表形式。
    b) 找到所有的起点，用HashMap来帮助记录每个节点的入度
  2. 创建图，找到每个节点的入度
    a) 利用输入，把图建好，然后遍历一下图，将入度信息记录在HashMap中
  3. 找所有的起点
    a) 所有入度为0的节点，都是有效的起点，而且我们讲他们都加入到一个队列中
  4. 排序
    a) 对每个起点，执行以下步骤
    —i) 把它加到结果的顺序中
    — ii)将其在图中的孩子节点取到
    — iii)将其孩子的入度减少1
    — iv)如果孩子的入度变为0，则改孩子节点成为起点，将其加入队列中
    b) 重复（a）过程，直到起点队列为空。

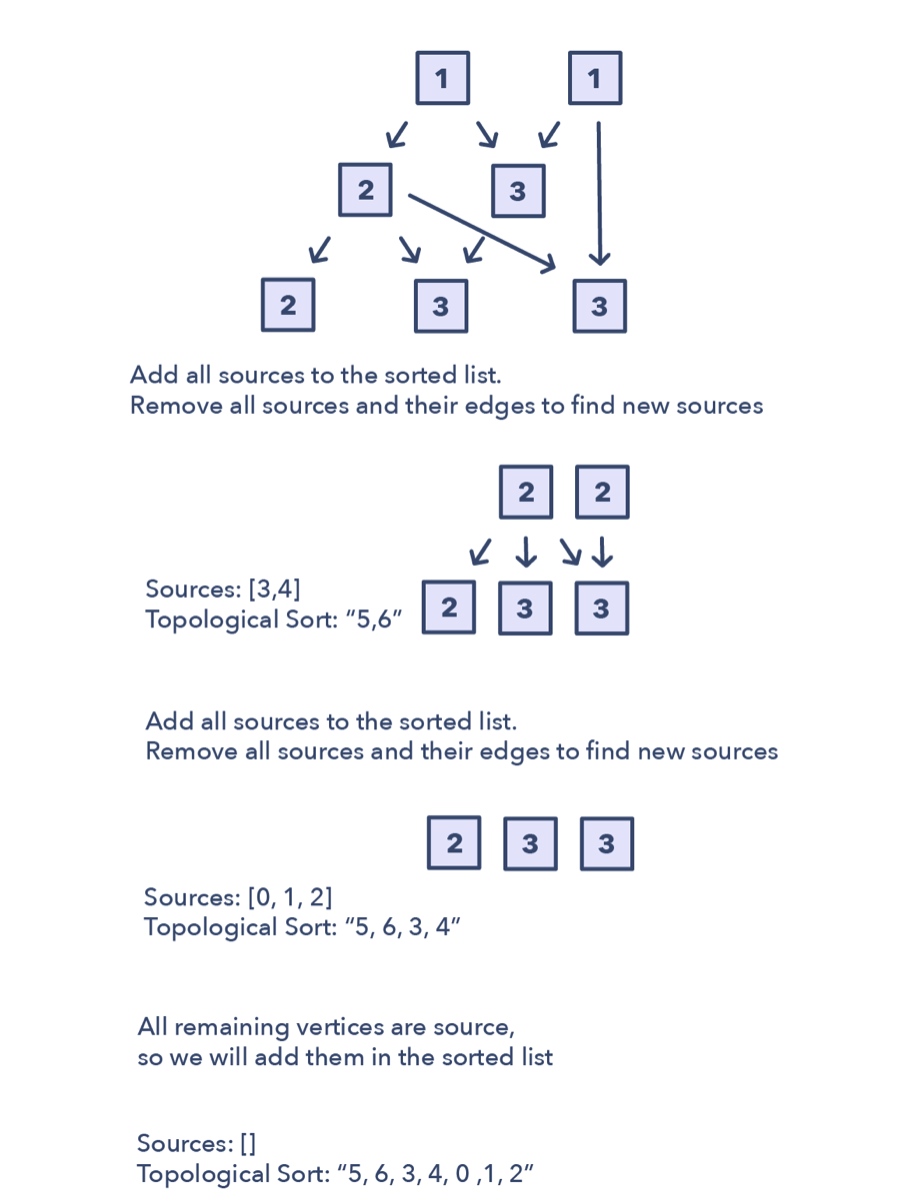
Topological

拓扑排序的主要标志
  1. 需要处理的图是无环图
  2. 需要以一定的顺序更新节点
  3. 需要处理的数据输入遵循某种规律
主要问题
  1. Task scheduling (medium)
  2. Minimum height of a tree (hard)

参考

关于算法的一点总结 | 一亩三分地

14 Patterns to Ace Any Coding Interview Question