LC105 Construct Binary Tree from Preorder and Inorder Traversal

Problem

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

Return the following binary tree:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7
Think

递归，preorder首元素为根，以这个作为区分，可以得到左右子树的preorder和inorder

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    if(preorder.empty() || inorder.empty()) return NULL;
    TreeNode* root = new TreeNode(preorder[0]);
    int pos = distance(inorder.begin(), find(inorder.begin(), inorder.end(), preorder[0]));
    cout << pos << endl;
    vector<int> inorder1(inorder.begin(), inorder.begin() + pos);
    vector<int> inorder2(inorder.begin() + pos + 1, inorder.end());
    vector<int> preorder1(preorder.begin() + 1, preorder.begin() + pos + 1);
    vector<int> preorder2(preorder.begin() + pos + 1, preorder.end());
    root->left = buildTree(preorder1, inorder1);
    root->right = buildTree(preorder2, inorder2);
    return root;
}

LC106 Construct Binary Tree from Inorder and Postorder Traversal

Problem

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

1
2
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]

Return the following binary tree:

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7
Think

和上一题类似

Code 
1
2
3
4
5
6
7
8
9
10
11
12
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    if(postorder.empty() || inorder.empty()) return NULL;
    TreeNode* root = new TreeNode(postorder.back());
    int pos = distance(inorder.begin(), find(inorder.begin(), inorder.end(), postorder.back()));
    vector<int> inorder1(inorder.begin(), inorder.begin() + pos);
    vector<int> inorder2(inorder.begin() + pos + 1, inorder.end());
    vector<int> postorder1(postorder.begin(), postorder.begin() + pos);
    vector<int> postorder2(postorder.begin() + pos, postorder.end() - 1);
    root->left = buildTree(inorder1, postorder1);
    root->right = buildTree(inorder2, postorder2);
    return root;
}

LC108 Convert Sorted Array to Binary Search Tree

Problem

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5
Think

类似上一题

Code 
1
2
3
4
5
6
7
8
9
10
11
TreeNode* sortedArrayToBST(vector<int>& nums) {
    if(nums.empty()) return NULL;
    int n = nums.size();
    int mid = n / 2;
    TreeNode* root = new TreeNode(nums[mid]);
    vector<int> left(nums.begin(), nums.begin() + mid);
    vector<int> right(nums.begin() + mid + 1, nums.end());
    root->left = sortedArrayToBST(left);
    root->right = sortedArrayToBST(right);
    return root;
}

LC109 Convert Sorted List to Binary Search Tree

Problem

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

1
2
3
4
5
6
7
8
9
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5
Think

采用类似于数组的方式，首先求出链表的长度，然后首先以当前节点建立一个一个节点，然后让左子节点等于left到mid - 1的部分求得的treenode，右子节点等于mid + 1到right的部分求得的treenode，在这里要注意由于里面需要使用链表节点，要先存储最初始的head节点。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
ListNode* head;
int getListSize(ListNode* head){
    int res = 0;
    ListNode* node = head;
    while(node){
        node = node->next;
        res++;
    }
    return res;
}
TreeNode* sortedListToBST(ListNode* head) {
    int len = getListSize(head);
    this->head = head;
    return helper(0, len - 1);
}
TreeNode* helper(int left, int right){
    if(left > right) return NULL;
    int mid = left + (right - left) / 2;
    TreeNode* tmp = helper(left, mid - 1);
    TreeNode* res = new TreeNode(this->head->val);
    res->left = tmp;
    this->head = this->head->next;
    res->right = helper(mid + 1, right);
    return res;
}

LC112 Path Sum

Problem

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

Think

递归DFS

Code 
1
2
3
4
5
bool hasPathSum(TreeNode* root, int sum) {
    if(!root) return false;
    if(!root->left && !root->right) return sum == root->val;
    return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}

LC113 Path Sum II

Problem

Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

Return:

1
2
3
4
[
   [5,4,11,2],
   [5,8,4,5]
]
Think

递归DFS，其中带上结果数组res

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<vector<int>> pathSum(TreeNode* root, int sum) {
    vector<vector<int>> res;
    if(!root) return res;
    helper(root, sum, {}, res);
    return res;
}
void helper(TreeNode* root, int sum, vector<int> path, vector<vector<int>> &res){
    if(!root) return;
    path.push_back(root->val);
    if(!root->left && !root->right){
        if(sum == root->val){
            res.push_back(path);
        }
        return;
    }
    sum -= root->val;
    helper(root->left, sum, path, res);
    helper(root->right, sum, path, res);
}

LC114 Flatten Binary Tree to Linked List

Problem

Given a binary tree, flatten it to a linked list in-place.

For example, given the following tree:

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

The flattened tree should look like:

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6
Think

递归，首先将左右子树flatten，然后将现在的右子树连到左子树最下方，将左子树置于当前节点的右子节点处即可。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
void flatten(TreeNode* root) {
    if(!root) return;
    flatten(root->left);
    flatten(root->right);
    if(!root->left) return;
    TreeNode* bottom = root->left;
    while(bottom->right){
        bottom = bottom->right;
    }
    bottom->right = root->right;
    root->right = root->left;
    root->left = NULL;
}

LC116 Populating Next Right Pointers in Each Node

Problem

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.
  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

img

1
2
3
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
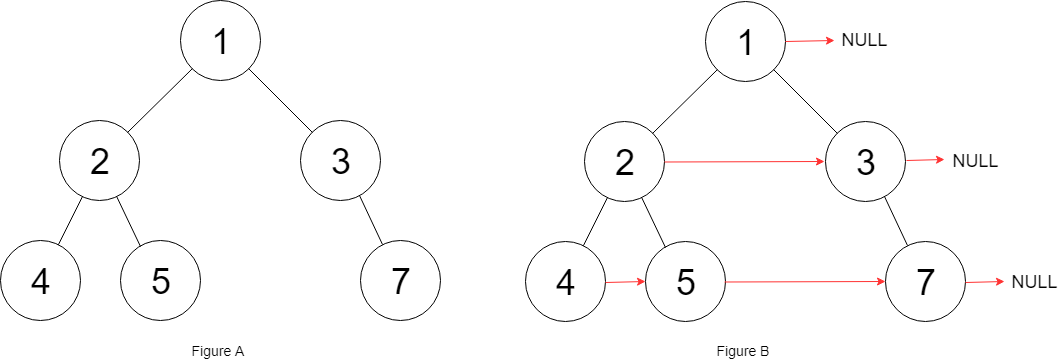
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

  • The number of nodes in the given tree is less than 4096.
  • -1000 <= node.val <= 1000
Think
  • Approach 1

BFS层序遍历

  • Approach 2

按层遍历，使用leftmost表示上一层的最左节点

Code
  • Approach 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Node* connect(Node* root) {
    if(!root) return NULL;
    queue<Node*> q;
    q.push(root);
    while(!q.empty()){
        int len = q.size();
        Node* pre = NULL;
        for(int i = 0; i < len; i++){
            Node* node = q.front();
            q.pop();
            if(pre != NULL) pre->next = node;
            pre = node;
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
    }
    return root;
}
  • Approach 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Node* connect(Node* root) {
    if(!root) return NULL;
    Node* leftmost = root;
    while(leftmost->left != NULL){
        Node* head = leftmost;
        while(head != NULL){
            head->left->next = head->right;
            if(head->next != NULL){
                head->right->next = head->next->left;
            }
            head = head->next;
        }
        leftmost = leftmost->left;
    }
    return root;
}

LC117 Populating Next Right Pointers in Each Node II

Problem

Given a binary tree

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.
  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

img

1
2
3
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

  • The number of nodes in the given tree is less than 6000.
  • -100 <= node.val <= 100
Think

BFS层序遍历

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Node* connect(Node* root) {
    if(!root) return NULL;
    queue<Node*> q;
    q.push(root);
    while(!q.empty()){
        int len = q.size();
        Node* pre = NULL;
        for(int i = 0; i < len; i++){
            Node* node = q.front();
            q.pop();
            if(pre != NULL) pre->next = node;
            pre = node;
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
    }
    return root;
}

LC124 Binary Tree Maximum Path Sum

Problem

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

1
2
3
4
5
6
7
Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

1
2
3
4
5
6
7
8
9
Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42
Think

可以转化为计算每一个节点处的最大左路径和最大右路径的和，再加上节点本身的值，因此可以使用一个递归函数来求解这个路径（某一个节点到叶节点的最大路径和）。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
int res = INT_MIN;
int maxGain(TreeNode* root){
    if(!root) return 0;
    int left = max(maxGain(root->left), 0);
    int right = max(maxGain(root->right), 0);
    int newPath = root->val + left + right;
    res = max(newPath, res);
    return root->val + max(left, right);
}
int maxPathSum(TreeNode* root) {
    maxGain(root);
    return res;
}

LC129 Sum Root to Leaf Numbers

Problem

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
Think

DFS递归，每次cur加上当前节点的值，然后乘上10传递给两个子树

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int sumNumbers(TreeNode* root) {
    if(!root) return 0;
    int res = 0;
    helper(root, 0, res);
    return res;
}
void helper(TreeNode* node, int cur, int &res){
    cur += node->val;
    if(!node->left && !node->right){
        res += cur;
        return;
    }
    if(node->left) helper(node->left, cur * 10, res);
    if(node->right) helper(node->right, cur * 10, res);
}

LC257 Binary Tree Paths

Problem

Given a binary tree, return all root-to-leaf paths.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
10
11
Input:

   1
 /   \
2     3
 \
  5

Output: ["1->2->5", "1->3"]

Explanation: All root-to-leaf paths are: 1->2->5, 1->3
Think

递归DFS

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<string> binaryTreePaths(TreeNode* root) {
    if(!root) return {};
    vector<string> res;
    helper(root, "", res);
    return res;
}
void helper(TreeNode* node, string cur, vector<string> &res){
    cur += "->" + to_string(node->val);
    if(!node->left && !node->right){
        res.push_back(cur.substr(2));
        return;
    }
    if(node->left) helper(node->left, cur, res);
    if(node->right) helper(node->right, cur, res);
}

LC332 Reconstruct Itinerary

Problem

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

  1. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
  2. All airports are represented by three capital letters (IATA code).
  3. You may assume all tickets form at least one valid itinerary.

Example 1:

1
2
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

Example 2:

1
2
3
4
Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
             But it is larger in lexical order.
Think

DFS + 栈，首先用multiset map存放每一条边，然后建立一个栈，首先将“JFK”存进栈，当栈不为空时：

设栈顶元素为s，如果map[t]为空，表明之后都不会再访问这个点，因此把这个点从栈中取出来放入结果数组中，否则将当前到达的节点放入栈中，并multiset map中删除对应元素

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<string> findItinerary(vector<vector<string>>& tickets) {
    vector<string> res;
    stack<string> st;
    st.push("JFK");
    unordered_map<string, multiset<string>> map;
    for(auto t: tickets){
        map[t[0]].insert(t[1]);
    }
    while(!st.empty()){
        string s = st.top();
        if(map[s].empty()){
            res.insert(res.begin(), s);
            st.pop();
        } else {
            st.push(*map[s].begin());
            map[s].erase(map[s].begin());
        }
    }
    return res;
}

LC337 House Robber III

Problem

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Determine the maximum amount of money the thief can rob tonight without alerting the police.

Example 1:

1
2
3
4
5
6
7
8
9
10
Input: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

Output: 7 
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

1
2
3
4
5
6
7
8
9
10
Input: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
Think

递归，当前节点node处开始抢，所能拿到的最大数值为node->val + ll + lr + rl + rr或者l + r

Code 
1
2
3
4
5
6
7
8
9
10
11
int rob(TreeNode* root) {
    int l = 0, r = 0;
    return helper(root, l, r);
}
int helper(TreeNode* node, int& l, int& r){
    if(!node) return 0;
    int ll = 0, lr = 0, rl = 0, rr = 0;
    l = helper(node->left, ll, lr);
    r = helper(node->right, rl, rr);
    return max(node->val + ll + lr + rl + rr, l + r);
}

LC394 Decode String

Problem

Given an encoded string, return its decoded string.

The encoding rule is: k[encoded_string], where the encoded_stringinside the square brackets is being repeated exactly k times. Note that kis guaranteed to be a positive integer.

You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.

Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there won’t be input like 3a or 2[4].

Example 1:

1
2
Input: s = "3[a]2[bc]"
Output: "aaabcbc"

Example 2:

1
2
Input: s = "3[a2[c]]"
Output: "accaccacc"

Example 3:

1
2
Input: s = "2[abc]3[cd]ef"
Output: "abcabccdcdcdef"

Example 4:

1
2
Input: s = "abc3[cd]xyz"
Output: "abccdcdcdxyz"
Think

递归，每一次的结果等于重复外围的数字次数的内部的内容，利用一个全局变量i来进行s的遍历。

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
string decodeString(string s) {
    int i = 0;
    return helper(s, i);
}
string helper(string s, int& i){
    string res;
    while(i < s.size() && s[i] != ']'){
        if(!isdigit(s[i])){
            res += s[i++];
        }
        else{
            int n = 0;
            while(i < s.size() && isdigit(s[i])) n = n * 10 + s[i++] - '0';
            i++;
            string repeat = helper(s, i);
            i++;
            for(int j = 0; j < n; j++){
                res += repeat;
            }
        }
    }
    return res;
}

Review

DFS一般是和递归联系起来的，主要包括如下内容的递归：

  1. 树上的递归，即左右子树存在相同的结构；
  2. 内部最小子结构的递归；