Breadth First Search(1)

LC107 Binary Tree Level Order Traversal II

Problem

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:
Given binary tree [3,9,20,null,null,15,7],
1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7
return its bottom-up level order traversal as:
1
2
3
4
5
[
  [15,7],
  [9,20],
  [3]
]

Think

层序遍历，然后翻转数组

Code

vector<vector<int>> levelOrderBottom(TreeNode* root) {
    if(!root) return {};
    queue<TreeNode*> s;
    s.push(root);
    vector<vector<int>> res;
    while(!s.empty()){
        int len = s.size();
        vector<int> cur;
        for(int i = 0; i < len; i++){
            TreeNode* node = s.front();
            cur.push_back(node->val);
            s.pop();
            if(node->left) s.push(node->left);
            if(node->right) s.push(node->right);
        }
        res.push_back(cur);
    }
    reverse(res.begin(), res.end());
    return res;
}

LC111 Minimum Depth of Binary Tree

Problem

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],
1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7
return its minimum depth = 2.

Think

Approach 1

递归，分别判断无左右子节点，只有左子节点，只有右子节点和有左右子节点

Approach 2

层序遍历BFS

Code

Approach 1

int minDepth(TreeNode* root) {
    if(!root) return 0;
    if(!root->left && !root->right) return 1;
    if(root->left && !root->right) return minDepth(root->left) + 1;
    if(!root->left && root->right) return minDepth(root->right) + 1;
    return min(minDepth(root->left), minDepth(root->right)) + 1;
}

Approach 2

int minDepth(TreeNode* root) {
    if(!root) return 0;
    queue<TreeNode*> q;
    q.push(root);
    int res = 1;
    while(!q.empty()){
        int len = q.size();
        for(int i = 0; i < len; i++){
            TreeNode* node = q.front();
            q.pop();
            if(!node->left && !node->right) return res;
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
        res++;
    }
    return 0;
}

LC126 Word Ladder II

Problem

Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

Only one letter can be changed at a time

Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

Note:

Return an empty list if there is no such transformation sequence.

All words have the same length.

All words contain only lowercase alphabetic characters.

You may assume no duplicates in the word list.

You may assume beginWord and endWord are non-empty and are not the same.

Example 1:
1
2
3
4
5
6
7
8
9
10
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output:
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]
Example 2:
1
2
3
4
5
6
7
8
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: []

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

Think

使用BFS遍历所有可能的路径path组成的paths队列。

首先初始化paths队列，将初始word所构成的路径放入；

当队列paths不为空时：

取出最前的一个路径；

如果该路径长度超过当前的level值，也就是当前应当遍历到第几层，则说明wordList中存在一些word已经出现在当前路径中，这些词不能再次出现在接下来的路径中，所以直接在wordList中删除这些词，并将level置为当前路径的长度；如果当前路径长度已经大于minLevel，则说明后面的所有路径都只会更长而不会更短，因此直接break；

取出当前路径的最后一个word，并以这个word作为起始word向后遍历，修改其中的一个字符，如果修改后的word存在于当前的wordList中，则将它加入当前路径；判断是否已经到达endWord，如果到达的话就直接加入res并更新minLevel值，否则加入paths中进行下一次的循环。

Code

vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    vector<vector<string>> res;
    unordered_set<string> wordDict(wordList.begin(), wordList.end());
    vector<string> p = {beginWord};
    queue<vector<string>> q;
    q.push(p);
    int level = 1, minLevel = INT_MAX;
    unordered_set<string> words;
    while(!q.empty()){
        vector<string> t = q.front();
        q.pop();
        if(t.size() > level){
            for(auto word: words) wordDict.erase(word);
            words.clear();
            level = t.size();
            if(level > minLevel) break;
        }

        string cur = t.back();
        for(int i = 0; i < cur.size(); i++){
            string next = cur;
            for(char c = 'a'; c <= 'z'; c++){
                next[i] = c;
                if(!wordDict.count(next)) continue;
                words.insert(next);
                vector<string> curPath = t;
                curPath.push_back(next);
                if(next == endWord){
                    res.push_back(curPath);
                    minLevel = level;
                }
                else{
                    q.push(curPath);
                }
            }
        }
    }
    return res;
}

LC127 Word Ladder

Problem

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

Only one letter can be changed at a time.

Each transformed word must exist in the word list.

Note:

Return 0 if there is no such transformation sequence.

All words have the same length.

All words contain only lowercase alphabetic characters.

You may assume no duplicates in the word list.

You may assume beginWord and endWord are non-empty and are not the same.

Example 1:
1
2
3
4
5
6
7
8
9
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output: 5

Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Example 2:
1
2
3
4
5
6
7
8
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: 0

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

Think

基础的BFS，注意遇到这种题要严格按照BFS的运行方式来思考，比如求最短路径之类的，要注意不要往Back Tracing上靠！！！

Code

int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
    unordered_set<string> wordDict(wordList.begin(), wordList.end());
    if(!wordDict.count(endWord)) return 0;
    queue<string> q;
    q.push(beginWord);
    unordered_set<string> visited;
    int level = 1, res = INT_MAX;
    while(!q.empty()){
        int len = q.size();
        level++;
        for(int i = 0; i < len; i++){
            string word = q.front();
            q.pop();
            for(int i = 0; i < word.size(); i++){
                string newWord = word;
                for(char c = 'a'; c <= 'z'; c++){
                    newWord[i] = c;
                    if(newWord == word) continue;
                    if(!wordDict.count(newWord)) continue;
                    if(visited.count(newWord)) continue;
                    if(newWord == endWord){
                        return level;
                    }
                    q.push(newWord);
                    visited.insert(newWord);
                }
            }
        }
    }
    return 0;
}

LC130 Surrounded Regions

Problem

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example:
1
2
3
4
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
1
2
3
4
X X X X
X X X X
X X X X
X O X X
Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Think

从每一条边上为O的地点出发，BFS或者DFS找到所有和这个O相连的O，将它们改成E（一方面标识哪些O是符合条件的，一方面作为visited数组使用），最后将所有的O改成X，E改成O。

Code

void solve(vector<vector<char>>& board) {
    if(board.empty() || board[0].empty()) return;
    int m = board.size(), n = board[0].size();
    // four borders
    // left border
    for(int i = 0; i < m; i++){
        BFS(board, i, 0);
    }
    // right border
    for(int i = 0; i < m; i++){
        BFS(board, i, n - 1);
    }
    // up border
    for(int i = 1; i < n - 1; i++){
        BFS(board, 0, i);
    }
    // bottom border
    for(int i = 1; i < n - 1; i++){
        BFS(board, m - 1, i);
    }

    for(int i = 0; i < m; i++){
        for(int j = 0; j < n; j++){
            if(board[i][j] == 'E'){
                board[i][j] = 'O';
            }
            else if(board[i][j] == 'O'){
                board[i][j] = 'X';
            }
        }
    }
}
void BFS(vector<vector<char>>& board, int row, int col){
    if(board[row][col] != 'O') return;
    int m = board.size(), n = board[0].size();
    int left[] = {-1, 0, 1, 0}, right[] = {0, -1, 0, 1};
    queue<pair<int, int>> q;
    q.push({row, col});
    while(!q.empty()){
        pair<int, int> cur = q.front();
        q.pop();
        if(cur.first < 0 || cur.first >= m || cur.second < 0 || cur.second >= n) continue;
        if(board[cur.first][cur.second] != 'O') continue;
        board[cur.first][cur.second] = 'E';
        for(int i = 0; i < 4; i++){
            q.push({cur.first + left[i], cur.second + right[i]});
        }
        
    }
}

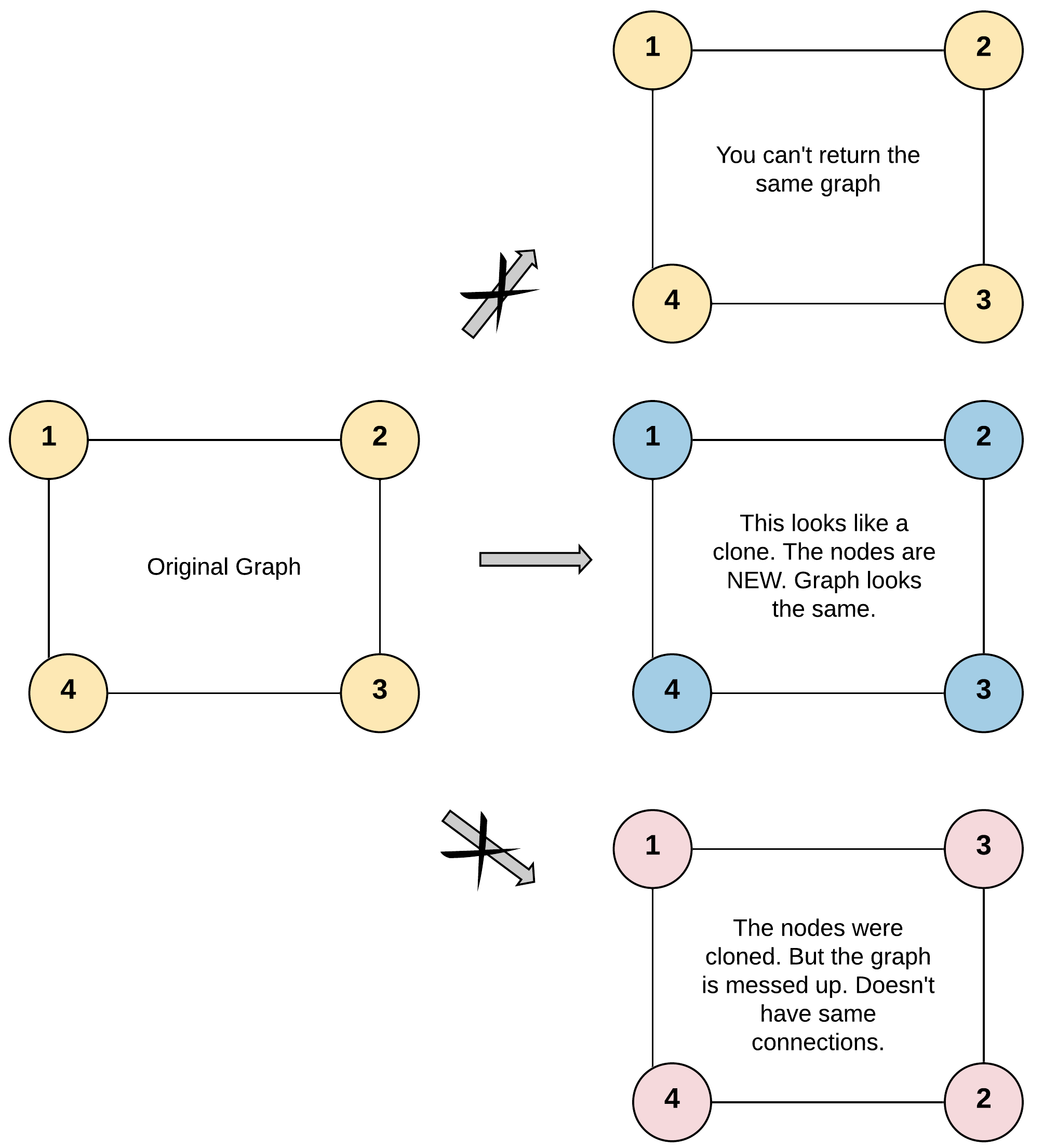
LC133 Clone Graph

Problem

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
1
2
3
4
class Node {
    public int val;
    public List<Node> neighbors;
}
Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:
1
2
3
4
5
6
7
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
1
2
3
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
1
2
3
Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.
Example 4:
1
2
Input: adjList = [[2],[1]]
Output: [[2],[1]]
Constraints:

1 <= Node.val <= 100

Node.val is unique for each node.

Number of Nodes will not exceed 100.

There is no repeated edges and no self-loops in the graph.

The Graph is connected and all nodes can be visited starting from the given node.

Think

BFS配合unordered_map，存放所有的节点对，最后返回根节点对应的节点即可。

Code

Node* cloneGraph(Node* node) {
    if(!node) return NULL;
    unordered_map<Node*, Node*> visited;
    queue<Node*> q;
    q.push(node);
    visited[node] = new Node(node->val);
    while(!q.empty()){
        Node* tmp = q.front();
        q.pop();
        for(Node* next: tmp->neighbors){
            if(!visited.count(next)){
                visited[next] = new Node(next->val);
                q.push(next);
            }
            visited[tmp]->neighbors.push_back(visited[next]);
        }
    }
    return visited[node];
}

LC199 Binary Tree Right Side View

Problem

Given a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Example:
1
2
3
4
5
6
7
8
9
Input: [1,2,3,null,5,null,4]
Output: [1, 3, 4]
Explanation:

   1            <---
 /   \
2     3         <---
 \     \
  5     4       <---

Think

树的BFS&层序，可以不用visited

Code

vector<int> rightSideView(TreeNode* root) {
    if(!root) return {};
    queue<TreeNode*> q;
    vector<int> res;
    q.push(root);
    while(!q.empty()){
        int len = q.size();
        for(int i = 0; i < len; i++){
            TreeNode* node = q.front();
            q.pop();
            if(i == len - 1) res.push_back(node->val);
            if(node->left) q.push(node->left);
            if(node->right) q.push(node->right);
        }
    }
    return res;
}

LC279 Perfect Squares

Problem

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

Example 1:
1
2
3
Input: n = 12
Output: 3 
Explanation: 12 = 4 + 4 + 4.
Example 2:
1
2
3
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

Think

DP，dp[i] = min(dp[i - j * j] + 1), for all j 满足j * j <= n

Code

int numSquares(int n) {
    vector<int> dp(n + 1, 0);
    dp[0] = 0;
    dp[1] = 1;
    for(int i = 2; i <= n; i++){
        int mx = sqrt(i);
        dp[i] = i;
        for(int j = 1; j <= mx; j++){
            dp[i] = min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

LC301 Remove Invalid Parentheses

Problem

Remove the minimum number of invalid parentheses in order to make the input string valid. Return all possible results.

Note: The input string may contain letters other than the parentheses ( and ).

Example 1:
1
2
Input: "()())()"
Output: ["()()()", "(())()"]
Example 2:
1
2
Input: "(a)())()"
Output: ["(a)()()", "(a())()"]
Example 3:
1
2
Input: ")("
Output: [""]

Think

BFS，遍历每一种可能的删减

Code

vector<string> removeInvalidParentheses(string s) {
    // if(isValid(s)) return {s};
    queue<string> q;
    q.push(s);
    unordered_set<string> visited;
    while(!q.empty()){
        int len = q.size();
        vector<string> res;
        for(int i = 0; i < len; i++){
            string str = q.front();
            q.pop();
            if(isValid(str)){
                res.push_back(str);
            }
            for(int j = 0; j < str.size(); j++){
                if(str[j] != '(' && str[j] != ')') continue;
                string newString = str.substr(0, j) + str.substr(j + 1);
                if(!visited.count(newString)){
                    q.push(newString);
                    visited.insert(newString);
                }
            }
        }
        if(!res.empty()){
            // vector<string> ret(res.begin(), res.end());
            return res;
        }
    }
    return {s};
}
bool isValid(string s){
    int idx = 0;
    for(char c: s){
        if(c == '('){
            idx++;
        }
        else if(c ==')'){
            if(idx == 0) return false;
            idx--;
        }
    }
    return idx == 0;
}

LC310 Minimum Height Trees

Problem

For an undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.

Format
The graph contains n nodes which are labeled from 0 to n - 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).

You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

Example 1 :
1
2
3
4
5
6
7
8
9
Input: n = 4, edges = [[1, 0], [1, 2], [1, 3]]

        0
        |
        1
       / \
      2   3 

Output: [1]
Example 2 :
1
2
3
4
5
6
7
8
9
10
11
Input: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]

     0  1  2
      \ | /
        3
        |
        4
        |
        5 

Output: [3, 4]
Note:

According to the definition of tree on Wikipedia: “a tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.”

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Think

BFS，但是这一题的BFS不是从根节点开始，而是从所有的叶节点开始遍历，然后每次都将这些叶节点从图中删去（也就是将连接到它们的边的另一个端的节点处的记录删去），从而实现从下到上每次都删去一层叶节点的操作，最终剩下的1个或者两个节点就是我们要求解的结果。

Code

vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
    if(n == 1) return {0};
    vector<unordered_set<int>> adj(n);
    queue<int> q;
    for(auto e: edges){
        adj[e[0]].insert(e[1]);
        adj[e[1]].insert(e[0]);
    }
    for(int i = 0; i < n; i++){
        if(adj[i].size() == 1) q.push(i);
    }
    while(n > 2){
        int len = q.size();
        n -= len;
        for(int i = 0; i < len; i++){
            int cur = q.front();
            q.pop();
            for(auto next: adj[cur]){
                adj[next].erase(cur);
                if(adj[next].size() == 1) q.push(next);
            }
        }
    }
    vector<int> res;
    while(!q.empty()){
        res.push_back(q.front());
        q.pop();
    }
    return res;
}

LC417 Pacific Atlantic Water Flow

Problem

Given an m x n matrix of non-negative integers representing the height of each unit cell in a continent, the “Pacific ocean” touches the left and top edges of the matrix and the “Atlantic ocean” touches the right and bottom edges.

Water can only flow in four directions (up, down, left, or right) from a cell to another one with height equal or lower.

Find the list of grid coordinates where water can flow to both the Pacific and Atlantic ocean.

Note:

The order of returned grid coordinates does not matter.

Both m and n are less than 150.

Example:
1
2
3
4
5
6
7
8
9
10
11
12
13
Given the following 5x5 matrix:

  Pacific ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * Atlantic

Return:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).

Think

BFS，首先分别将两个边的节点加入队列中，然后对两个队列进行BFS，只push数值变大的节点即可。

Code

vector<int> dx{-1, 0, 1, 0};
vector<int> dy{0, -1, 0, 1};
vector<vector<int>> pacificAtlantic(vector<vector<int>>& matrix) {
    if(matrix.empty() || matrix[0].empty()) return {};
    int m = matrix.size(), n = matrix[0].size();
    // four borders
    unordered_set<int> res1;
    unordered_set<int> res2;

    queue<vector<int>> q1;
    queue<vector<int>> q2;
    // left border
    for(int i = 0; i < m; i++) q1.push({i, 0});
    // up border
    for(int i = 1; i < n; i++) q1.push({0, i});
    // right border
    for(int i = 0; i < m - 1; i++) q2.push({i, n - 1});
    // bottom border
    for(int i = 0; i < n; i++) q2.push({m - 1, i});
    BFS(res1, matrix, q1);
    BFS(res2, matrix, q2);
    vector<vector<int>> res;
    for(auto r1: res1){
        if(res2.count(r1)) res.push_back({r1 / n, r1 % n});
    }
    return res;
}
void BFS(unordered_set<int>& res, vector<vector<int>>& matrix, queue<vector<int>>& q){
    int m = matrix.size(), n = matrix[0].size();
    unordered_set<int> visited;
    while(!q.empty()){
        int len = q.size();
        for(int i = 0; i < len; i++){
            vector<int> cur = q.front();
            q.pop();
            res.insert(cur[0] * n + cur[1]);
            int curValue = matrix[cur[0]][cur[1]];
            for(int j = 0; j < 4; j++){
                if((cur[0] + dx[j]) >= 0 && (cur[0] + dx[j]) < m && (cur[1] + dy[j]) >= 0 && (cur[1] + dy[j]) < n){
                    int next = matrix[cur[0] + dx[j]][cur[1] + dy[j]];
                    if(next >= curValue && !visited.count((cur[0] + dx[j]) * n + cur[1] + dy[j])){
                        q.push({cur[0] + dx[j], cur[1] + dy[j]});
                        visited.insert((cur[0] + dx[j]) * n + cur[1] + dy[j]);
                    }
                }
            }
        }
    }
}

LC513 Find Bottom Left Tree Value

Problem

Given a binary tree, find the leftmost value in the last row of the tree.

Example 1:
1
2
3
4
5
6
7
8
Input:

    2
   / \
  1   3

Output:
1
Example 2:
1
2
3
4
5
6
7
8
9
10
11
12
Input:

        1
       / \
      2   3
     /   / \
    4   5   6
       /
      7

Output:
7
Note: You may assume the tree (i.e., the given root node) is not NULL.

Think

BFS，但是在每一层上先加入右子节点，再加入左子节点，这样最后一次从queue里pop出来的就是要求的最底下一层的最左边的点。

Code

int findBottomLeftValue(TreeNode* root) {
    queue<TreeNode*> q;
    q.push(root);
    TreeNode* node;
    while(!q.empty()){
        node = q.front();
        q.pop();
        if(node->right) q.push(node->right);
        if(node->left) q.push(node->left);
    }
    return node->val;
}

LC515 Find Largest Value in Each Tree Row

Problem

You need to find the largest value in each row of a binary tree.

Example:

Input: 

          1
         / \
        3   2
       / \   \  
      5   3   9 

Output: [1, 3, 9]

Think

BFS+层序遍历，每层求最大值即可

Code

vector<int> largestValues(TreeNode* root) {
    if(!root) return {};
    vector<int> res;
    queue<TreeNode*> q;
    q.push(root);
    while(!q.empty()){
        int len = q.size();
        int cur = INT_MIN;
        for(int i = 0; i < len; i++){
            TreeNode* node = q.front();
            q.pop();
            cur = max(cur, node->val);
            if(node->right) q.push(node->right);
            if(node->left) q.push(node->left);
        }
        res.push_back(cur);
    }
    return res;
}

LC529 Minesweeper

Problem

Let’s play the minesweeper game (Wikipedia, online game)!

You are given a 2D char matrix representing the game board. ‘M’ represents an unrevealed mine, ‘E’ represents an unrevealed empty square, ‘B’ represents a revealed blank square that has no adjacent (above, below, left, right, and all 4 diagonals) mines, digit (‘1’ to ‘8’) represents how many mines are adjacent to this revealed square, and finally ‘X’ represents a revealed mine.

Now given the next click position (row and column indices) among all the unrevealed squares (‘M’ or ‘E’), return the board after revealing this position according to the following rules:

If a mine (‘M’) is revealed, then the game is over - change it to ‘X’.

If an empty square (‘E’) with no adjacent mines is revealed, then change it to revealed blank (‘B’) and all of its adjacent unrevealed squares should be revealed recursively.

If an empty square (‘E’) with at least one adjacent mine is revealed, then change it to a digit (‘1’ to ‘8’) representing the number of adjacent mines.

Return the board when no more squares will be revealed.

Example 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: 

[['E', 'E', 'E', 'E', 'E'],
 ['E', 'E', 'M', 'E', 'E'],
 ['E', 'E', 'E', 'E', 'E'],
 ['E', 'E', 'E', 'E', 'E']]

Click : [3,0]

Output: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'M', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]
Example 2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'M', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]

Click : [1,2]

Output: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'X', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]
Note:

The range of the input matrix’s height and width is [1,50].

The click position will only be an unrevealed square (‘M’ or ‘E’), which also means the input board contains at least one clickable square.

The input board won’t be a stage when game is over (some mines have been revealed).

For simplicity, not mentioned rules should be ignored in this problem. For example, you don’t need to reveal all the unrevealed mines when the game is over, consider any cases that you will win the game or flag any squares.

Think

BFS，首先判断click处是否为M，是的话则改为X，然后直接返回

否则从click处bfs遍历整个图，对于遍历到的点，首先判断改点周围是否有M，有的话改为数字，否则改为B，并将周围八个点加入q

Code

vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
    vector<vector<char>> res = board;
    if(board[click[0]][click[1]] == 'M'){
        res[click[0]][click[1]] = 'X';
        return res;
    }
    int m = board.size(), n = board[0].size();
    vector<int> dx = {-1, -1, -1, 0, 0, 1, 1, 1};
    vector<int> dy = {-1, 0, 1, -1, 1, -1, 0, 1};
    queue<vector<int>> q;
    unordered_set<int> visited;
    q.push(click);
    while(!q.empty()){
        vector<int> cur = q.front();
        q.pop();
        if(board[cur[0]][cur[1]] == 'E'){
            int cnt = 0;
            for(int i = 0; i < 8; i++){
                if(cur[0] + dx[i] >= 0 && cur[0] + dx[i] < m && cur[1] + dy[i] >= 0 && cur[1] + dy[i] < n){
                    if(board[cur[0] + dx[i]][cur[1] + dy[i]] == 'M') cnt++;
                }
            }
            if(cnt == 0){
                res[cur[0]][cur[1]] = 'B';
                for(int i = 0; i < 8; i++){
                    if(cur[0] + dx[i] >= 0 && cur[0] + dx[i] < m && cur[1] + dy[i] >= 0 && cur[1] + dy[i] < n){
                        if(board[cur[0] + dx[i]][cur[1] + dy[i]] == 'E'){
                            if(!visited.count((cur[0] + dx[i]) * n + cur[1] + dy[i])){
                                visited.insert((cur[0] + dx[i]) * n + cur[1] + dy[i]);
                                q.push({cur[0] + dx[i], cur[1] + dy[i]});
                            }
                        }
                    }
                }
                
            }
            else res[cur[0]][cur[1]] = (char)(cnt + '0');
        }
    }
    return res;
}

LC542 01 Matrix

Problem

Given a matrix consists of 0 and 1, find the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:
1
2
3
4
5
6
7
8
9
Input:
[[0,0,0],
 [0,1,0],
 [0,0,0]]

Output:
[[0,0,0],
 [0,1,0],
 [0,0,0]]
Example 2:
1
2
3
4
5
6
7
8
9
Input:
[[0,0,0],
 [0,1,0],
 [1,1,1]]

Output:
[[0,0,0],
 [0,1,0],
 [1,2,1]]
Note:

The number of elements of the given matrix will not exceed 10,000.

There are at least one 0 in the given matrix.

The cells are adjacent in only four directions: up, down, left and right.

Think

Approach 1

BFS，首先将所有的0的位置加入队列，从这些0开始遍历matrix，如果遍历到的1处的值大于当前得到的路径的长度，则更新，并将该点加入队列。

Approach 2

两次DP，分别从左上角和右下角出发

左上角：dp[i, j] = min(dp[i, j - 1] + 1, dp[i - 1, j] + 1)

右下角：dp[i, j] = min(dp[i, j + 1] + 1, dp[i + 1, j] + 1)

注意在初始化结果数组的时候，res中的每个值都必须初始化成INT_MAX - 10000，因为在第一次遍历过程中可能存在INT_MAX + 1的操作，而最长路径不可能超过10000（题目中说matrix的边长最大为10000）。

Code

Approach 1

vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
    if(matrix.empty() || matrix[0].empty()) return matrix;
    int m = matrix.size(), n = matrix[0].size();
    queue<vector<int>> q;
    vector<vector<int>> res(m, vector<int>(n, INT_MAX));
    for(int i = 0; i < m; i++){
        for(int j = 0; j < n; j++){
            if(matrix[i][j] == 0){
                res[i][j] = 0;
                q.push({i, j});
            }
        }
    }
    vector<int> dx = {0, 1, 0, -1}, dy = {1, 0, -1, 0};
    while(!q.empty()){
        vector<int> cur = q.front();
        q.pop();
        for(int i = 0; i < 4; i++){
            if(cur[0] + dx[i] >= 0 && cur[0] + dx[i] < m && cur[1] + dy[i] >= 0 && cur[1] + dy[i] < n){
                if(res[cur[0] + dx[i]][cur[1] + dy[i]] > res[cur[0]][cur[1]] + 1){
                    res[cur[0] + dx[i]][cur[1] + dy[i]] = res[cur[0]][cur[1]] + 1;
                    q.push({cur[0] + dx[i], cur[1] + dy[i]});
                }
            }
        }
    }
    return res;
}

Approach 2

vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
    if(matrix.empty() || matrix[0].empty()) return matrix;
    int m = matrix.size(), n = matrix[0].size();
    queue<vector<int>> q;
    vector<vector<int>> res(m, vector<int>(n, INT_MAX - 10000));
    for(int i = 0; i < m; i++){
        for(int j = 0; j < n; j++){
            if(matrix[i][j] == 0){
                res[i][j] = 0;
            }
            else{
                if(i > 0) res[i][j] = min(res[i][j], res[i - 1][j] + 1);
                if(j > 0) res[i][j] = min(res[i][j], res[i][j - 1] + 1);
            }
        }
    }
    for(int i = m - 1; i >= 0; i--){
        for(int j = n - 1; j >= 0; j--){
            if(i < m - 1) res[i][j] = min(res[i][j], res[i + 1][j] + 1);
            if(j < n - 1) res[i][j] = min(res[i][j], res[i][j + 1] + 1);
        }
    }
    return res;
}

Review

BFS主要适用于求解最短路径，最短长度等一类最短问题，多和层序遍历配合使用，以达到可以求解路径长度的作用。需要注意如下：

起始节点不一定只有一个，可能是原数组或者图中的一类节点；
不一定非要从根节点出发来进行BFS，任意节点都可以作为BFS的出发的节点；
visited数组：在添加子节点进queue的同时添加进visited数组；
BFS可以进行层的删除，通过一层一层的删除叶节点来得到最终的中心点；
！！！！千万不要写成back tracing，回溯一般是用在要求得所有结果的情况下，类似DFS。

Yiming

Coding for fun ~

Breadth First Search(1)

LC107 Binary Tree Level Order Traversal II

LC111 Minimum Depth of Binary Tree

LC126 Word Ladder II

LC127 Word Ladder

LC130 Surrounded Regions

LC133 Clone Graph

LC199 Binary Tree Right Side View

LC279 Perfect Squares

LC301 Remove Invalid Parentheses

LC310 Minimum Height Trees

LC417 Pacific Atlantic Water Flow

LC513 Find Bottom Left Tree Value

LC515 Find Largest Value in Each Tree Row

LC529 Minesweeper

LC542 01 Matrix

Review